Example scripts¶
Showing 3D Directional Sensitivity¶
The 3d_dtcwt_directionality.py script in the examples directory shows how one may demonstrate the directional sensitivity of the 3D DT-CWT complex subband coefficients. It computes empirically the maximally sensitive directions for each subband and plots them in an interactive figure using matplotlib. A screenshot is reproduced below:
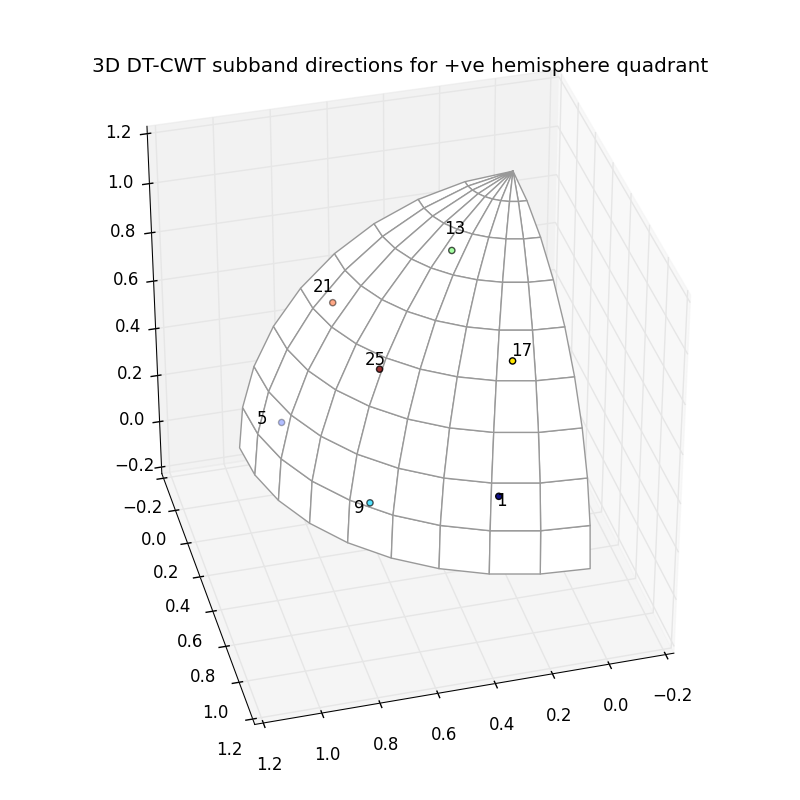
There are some points to note about this diagram. Each subband is labeled sich that ‘1’ refers to the first subband, ‘5’ the fifth and so forth. On this diagram the subbands are all four apart reflecting the fact that, for example, subbands 2, 3 and 4 are positioned in the other four quadrants of the upper hemisphere reflecting the position of subband 1. There are seven visible subband directions in the +ve quadrant of the hemisphere and hence there are 28 directions in total over all four quadrants.
The source for the script is shown below:
#!/bin/python
"""
An example of the directional selectivity of 3D DT-CWT coefficients.
This example creates a 3D array holding an image of a sphere and performs the
3D DT-CWT transform on it. The locations of maxima (and their images about the
mid-point of the image) are determined for each complex coefficient at level 2.
These maxima points are then shown on a single plot to demonstrate the
directions in which the 3D DT-CWT transform is selective.
"""
# Import the libraries we need
from matplotlib.pyplot import *
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
from dtcwt import dtwavexfm3, dtwaveifm3, biort, qshift
# Specify details about sphere and grid size
GRID_SIZE = 128
SPHERE_RAD = int(0.45 * GRID_SIZE) + 0.5
# Compute an image of the sphere
grid = np.arange(-(GRID_SIZE>>1), GRID_SIZE>>1)
X, Y, Z = np.meshgrid(grid, grid, grid)
r = np.sqrt(X*X + Y*Y + Z*Z)
sphere = (0.5 + np.clip(SPHERE_RAD-r, -0.5, 0.5)).astype(np.float32)
# Specify number of levels and wavelet family to use
nlevels = 2
b = biort('near_sym_a')
q = qshift('qshift_a')
# Form the DT-CWT of the sphere. We use discard_level_1 since we're
# uninterested in the inverse transform and this saves us some memory.
Yl, Yh = dtwavexfm3(sphere, nlevels, b, q, discard_level_1=True)
# Plot maxima
figure(figsize=(8,8))
ax = gcf().add_subplot(1,1,1, projection='3d')
ax.set_aspect('equal')
ax.view_init(35, 75)
# Plot unit sphere +ve octant
thetas = np.linspace(0, np.pi/2, 10)
phis = np.linspace(0, np.pi/2, 10)
def sphere_to_xyz(r, theta, phi):
st, ct = np.sin(theta), np.cos(theta)
sp, cp = np.sin(phi), np.cos(phi)
return r * np.asarray((st*cp, st*sp, ct))
tris = []
rad = 0.99 # so that points plotted latter are not z-clipped
for t1, t2 in zip(thetas[:-1], thetas[1:]):
for p1, p2 in zip(phis[:-1], phis[1:]):
tris.append([
sphere_to_xyz(rad, t1, p1),
sphere_to_xyz(rad, t1, p2),
sphere_to_xyz(rad, t2, p2),
sphere_to_xyz(rad, t2, p1),
])
sphere = Poly3DCollection(tris, facecolor='w', edgecolor=(0.6,0.6,0.6))
ax.add_collection3d(sphere)
locs = []
scale = 1.1
for idx in xrange(Yh[-1].shape[3]):
Z = Yh[-1][:,:,:,idx]
C = np.abs(Z)
max_loc = np.asarray(np.unravel_index(np.argmax(C), C.shape)) - np.asarray(C.shape)*0.5
max_loc /= np.sqrt(np.sum(max_loc * max_loc))
# Only record directions in the +ve octant (or those from the -ve quadrant
# which can be flipped).
if np.all(np.sign(max_loc) == 1):
locs.append(max_loc)
ax.text(max_loc[0] * scale, max_loc[1] * scale, max_loc[2] * scale, str(idx+1))
elif np.all(np.sign(max_loc) == -1):
locs.append(-max_loc)
ax.text(-max_loc[0] * scale, -max_loc[1] * scale, -max_loc[2] * scale, str(idx+1))
# Plot all directions as a scatter plot
locs = np.asarray(locs)
ax.scatter(locs[:,0], locs[:,1], locs[:,2], c=np.arange(locs.shape[0]))
w = 1.1
ax.auto_scale_xyz([0, w], [0, w], [0, w])
legend()
title('3D DT-CWT subband directions for +ve hemisphere quadrant')
tight_layout()
show()
# vim:sw=4:sts=4:et