3D transform¶
In the examples below I assume you’ve imported pyplot and numpy and, of course,
the dtcwt library itself
from matplotlib.pylab import *
import dtcwt
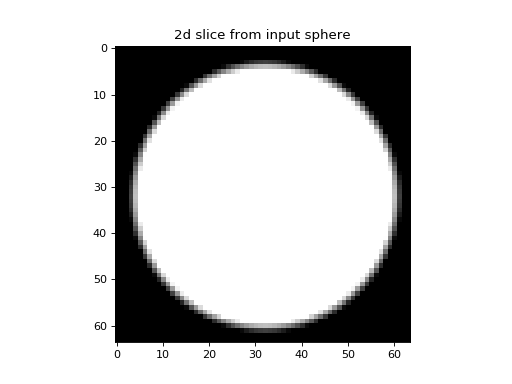
We can demonstrate the 3D transform by generating a 64x64x64 array which contains the image of a sphere
GRID_SIZE = 64
SPHERE_RAD = int(0.45 * GRID_SIZE) + 0.5
grid = np.arange(-(GRID_SIZE>>1), GRID_SIZE>>1)
X, Y, Z = np.meshgrid(grid, grid, grid)
r = np.sqrt(X*X + Y*Y + Z*Z)
sphere = 0.5 + 0.5 * np.clip(SPHERE_RAD-r, -1, 1)
trans = dtcwt.Transform3d()
sphere_t = trans.forward(sphere, nlevels=2)
The function returns a dtcwt.Pyramid instance containing the
lowpass image and a tuple of complex highpass coefficients
>>> print(sphere_t.lowpass.shape)
(16, 16, 16)
>>> for highpasses in sphere_t.highpasses:
... print(highpasses.shape)
(32, 32, 32, 28)
(16, 16, 16, 28)
(8, 8, 8, 28)
Performing the inverse transform should result in perfect reconstruction
>>> Z = trans.inverse(sphere_t)
>>> print(np.abs(Z - sphere).max()) # Should be < 1e-12
8.881784197e-15
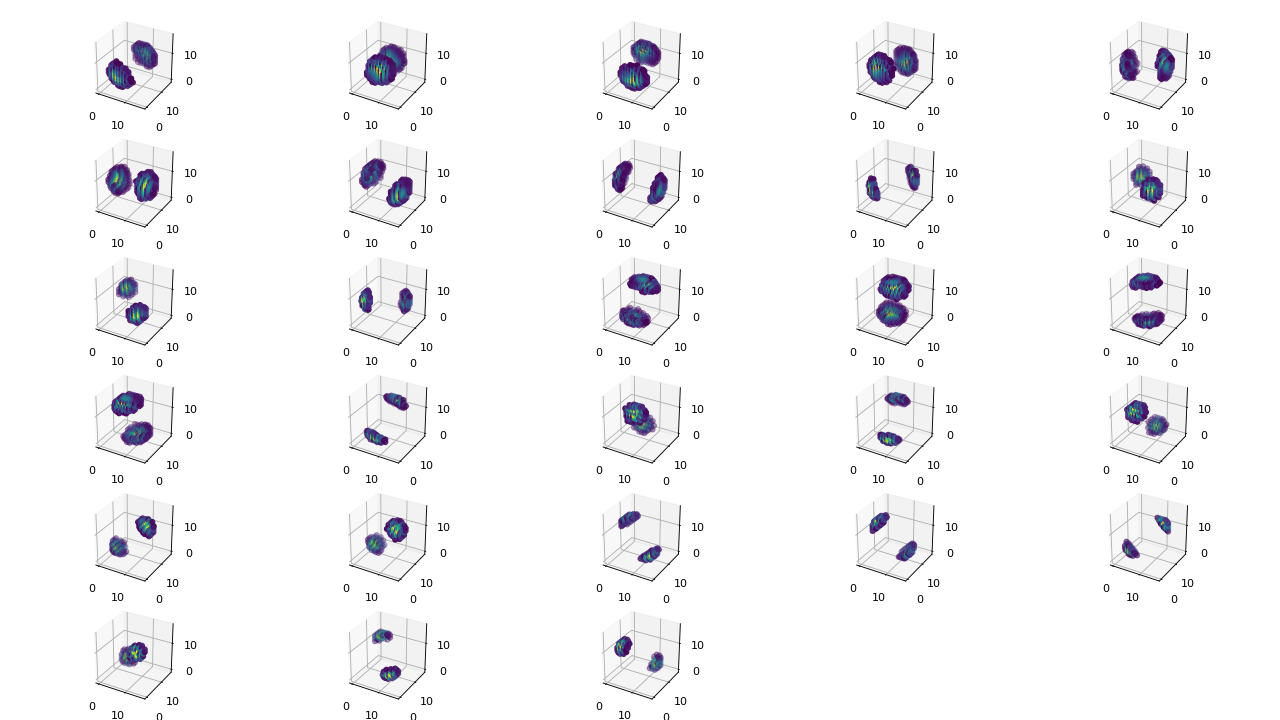
If you plot the locations of the large complex coefficients, you can see the directional sensitivity of the transform
from mpl_toolkits.mplot3d import Axes3D
figure()
imshow(sphere[:,:,GRID_SIZE>>1], interpolation='none', cmap=cm.gray)
title('2d slice from input sphere')
# Plot large magnitude wavelet coefficients' position in 3D.
figure(figsize=(16,9))
Yh = sphere_t.highpasses
nplts = Yh[-1].shape[3]
nrows = np.ceil(np.sqrt(nplts))
ncols = np.ceil(nplts / nrows)
W = np.max(Yh[-1].shape[:3])
for idx in range(Yh[-1].shape[3]):
C = np.abs(Yh[-1][:,:,:,idx])
ax = gcf().add_subplot(nrows, ncols, idx+1, projection='3d')
ax.set_aspect('equal')
good = C > 0.2*C.max()
x,y,z = np.nonzero(good)
ax.scatter(x, y, z, c=C[good].ravel())
ax.auto_scale_xyz((0,W), (0,W), (0,W))
tight_layout()
For a further directional sensitivity example, see Showing 3D Directional Sensitivity.